eventi vulcanici e sismici 2015

di seguito trovate i link ad articoli che trattano di due importanti eventi recenti:
 l'eruzione del vulcano cileno Calbuco e
 il forte terremoto del Nepal


http://www.ilfattoquotidiano.it/2015/04/23/cile-eruzione-spettacolare-vulcano-calbuco-regione-dei-laghi-era-inattivo-42-anni-allerta-in-argentina/1616014/2/#foto

http://video.corriere.it/eruzione-vulcano-calbuco-spettacolari-immagini-colonna-fumo-cenere-alta-15-chilometri/ffab40a6-ea97-11e4-850d-dfc1f9b6f2f5

http://www.repubblica.it/ambiente/2015/04/23/foto/cile_erutta_il_vulcano_calbuco_era_inattivo_da_42_anni-112620802/1/#1


http://www.corriere.it/esteri/15_aprile_26/terremoto-nepal-faglia-scontro-titanico-d861f8ee-ebe3-11e4-b9d3-aa4aa3ffc489.shtml

http://scienzenotizie.it/2015/05/12/terremoto-nepal-12-maggio-2015-nuova-violenta-scossa-di-magnitudo-7-4-richter-143108

http://www.adnkronos.com/fatti/esteri/2015/04/25/nepal-scienziati-ingv-una-delle-regioni-piu-alto-rischio-terremoti-nel-mondo_JedPsDBJVnfb2TDQ8hURSM.html

esercizi di preparazione all'esame

Esercizi di preparazione all’esame

Probabilità ( calcola le probabilità in frazione e in percentuale, indica l’evento più probabile e quello meno, indica quali sono gli eventi certi e quelli impossibili )

1.       calcola, la probabilità che estraendo un gettone della tombola questo sia:

-          Un numero dispari

-          Un numero minore di 10

-          Il numero 43

-          Un numero divisibile per dieci

-          Un numero multiplo di 20

2.       Un sacchetto contiene 20 palline blu, 10 rosse, 1 nera,12 gialle,2 viola. Calcola la probabilità che estraendo una pallina questa sia:

-          Blu

-          Un colore primario

-          Rossa o gialla

-          Nera o viola

-          Arancione

3.       Da un mazzo di 40 carte se ne estrae una a caso, calcola la probabilità che sia:

-          Un asso

-          Un numero minore di tre

-          Una figura

-          Un re

-          Una carta di cuori

-          Una carta nera

4.       In un sacchetto ci sono 13 dischetti bianchi, 2 neri, 4 gialli, 8 viola. Estraendone uno calcola la probabilità che sia:

-          Bianco

-          Di colore scuro

-          Nero o giallo

-          Verde

Proporzionalità (date le seguenti tabelle relative a due grandezze X e Y: completale, descrivi se si tratta di proporzionalità diretta o inversa, rappresentale sul piano cartesiano e scrivi l’equazione matematica corrispondente)

X	20	30	40	45	58	80	100	120
Y	40		80				200

X	30	50	60	100	150
Y	15	25			75

X	1	2	3	4	5	6
Y	60		20		12	10

Equazioni (risolvi,verifica e discuti le seguenti equazioni)

28-x=3

x-2-4=10

6x=-12

3(2x+7)=45

25x+40=140

12x+6=4

2+(3x+1)-3=5(x-1)

4(x-7)-2(x+5)=3x

5(x+1)=(2x+4)+3x

3(x-1)=3x-3

2(x+3)-6=2x

3x+2 – 2x-1 = 2x - 1

  3          2         3    6

(4+x)(4-x)+12=18-x²

(3x+1)(3x-1)+2=9x²+8x-3

Geometria solida (risolvi i seguenti problemi relativi a poliedri)

La superficie totale di una piramide quadrangolare regolare è di 4704 cm quadrati. Il lato di base è 6/5 dell’apotema e la loro somma è di 77 cm. Calcola:

a)      L’area di base della piramide

b)      La superficie laterale della piramide

c)       Il volume della piramide

d)      Il peso della piramide, che è di legno ( Ps =0,75 )

Sapendo che un cubo è equivalente a 1/6 della piramide, calcola:

e)      La superficie totale del cubo

In un trapezio isoscele ABCD la base maggiore AB è 5,5 cm, la base minore DC e l’altezza DH sono, rispettivamente, 5/11 e 4/11 della base maggiore. Calcola:

a)      Il perimetro e l’area del trapezio

b)      La superficie totale ed il volume di un prisma alto 6,28 cm che ha per base il trapezio isoscele

c)       Il peso del prisma, supponendo che sia costruito in legno d’abete ( Ps = 0,5 )

In un rettangolo la base misura 8 cm e l’altezza èi ¾  della base. Calcola:

a)      Il perimetro,  l’area e la diagonale del rettangolo

b)      La superficie totale e il volume di un parallelepipedo retto rettangolo che ha per base il rettangolo, sapendo che l’altezza del parallelepipedo è 5/3 dell’ altezza del rettangolo

c)       Lo spigolo di base di una piramide quadrangolare regolare, alta 12 cm, sapendo che è equivalente a 27/10 del parallelepipedo

programmi d'esame di matematica e scienze

ANNO SCOLASTICO 2014-2015, CLASSE TERZA D

PROGRAMMA DI ALGEBRA

1)      INSIEME DEI NUMERI REALI RELATIVI:

a)      concetto di numero reale

b)      l’insieme R, Q e N

c)        confronto e ordinamento sulla retta dei numeri relativi

d)       le quattro operazioni e l’elevamento a potenza nell’insieme R

2)      IL CALCOLO LETTERALE:

a)      utilizzo delle lettere per generalizzare il calcolo

b)       grado di un monomio

c)       somma algebrica di monomi e polinomi

d)      prodotto tra monomi e polinomi

e)       elevamento a potenza di un monomio

f)        Espressioni con monomi e polinomi

g)      Utilizzo di un polinomio per esprimere aree e perimetri

3)      RISOLUZIONE DI EQUAZIONI:

a)      Concetto di uguaglianza tra espressioni letterali

b)      Concetto di incognita

c)       Principi di equivalenza

d)      Risoluzione di equazioni di primo grado intere

e)      Risoluzione di equazioni a termini frazionari

f)       Verifica e discussione di un’equazione

4)      PROPORZIONALITA’

a)      concetto di proporzionalità diretta e inversa

b)      rappresentazione grafica della proporzionalità

c)       il peso specifico dei solidi

5)      PROBABILITA’

a)      concetto di probabilità

b)      evento certo e impossibile

c)       problemi sul calcolo della probabilità semplice

d)      probabilità espressa in frazione e in percentuale

6)      STATISTICA

a)      Dati statistici, frequenza assoluta e relativa

b)      Indicatori statistici: moda, media ,mediana

PROGRAMMA DI GEOMETRIA

1)      CIRCONFERENZA E CERCHIO

a)      Definizione di circonferenza e cerchio

b)      Corde e diametro, distanza di una corda dal centro

c)       Misura della circonferenza

d)      Angoli al centro e alla circonferenza

e)      Area del cerchio e delle sue parti

f)       poligoni  inscrittibili e circoscrittibili

2)      POLIEDRI

a)      Introduzione alla geometria solida: concetto di tridimensionalità e volume

b)      Prisma retto: area di base, laterale, totale, volume

c)       Parallelepipedo : area di base, laterale, totale ,volume, diagonale

d)      Cubo: area di base, laterale, totale, volume, diagonale

e)      Piramide retta: area di base, laterale, totale, volume, misura dell’apotema

f)       equivalenza tra poliedri

PROGRAMMA DI SCIENZE

1)      CHIMICA

a)      Struttura atomica

b)      Fissione e fusione nucleare

2)      UNIVERSO E SISTEMA SOLARE

a)      Corpi celesti: stelle e pianeti

b)      Composizione e vita di una stella

c)       Origine e d espansione dell’universo: teoria del big-bang

d)      Composizione del sistema solare: il sole e i pianeti

e)      Satelliti, asteroidi, meteore e comete

f)       Forza di gravità

3)      TERRA E LUNA

a)      composizione interna della terra e fenomeni endogeni

b)      vulcani e terremoti

c)       moti terrestri e loro conseguenze

d)      moti lunari e loro conseguenze

e)      ipotesi sull’origine del nostro satellite

4)      EVOLUZIONE DELLA CROSTA TERRESTRE

a)      Teoria della deriva dei continenti

b)      Tettonica delle placche

5)      IMPATTO ANTROPICO SULL’AMBIENTE

a)      Inquinamento dell’aria

b)      Inquinamento dell’acqua

c)       Inquinamento del suolo

d)      Protezione ambientale

formule circonferenza e cerchio

FORMULA DIRETTA	FORMULE INVERSE	SIGNIFICATO SIMBOLI
Lunghezza della circonferenza	C = 2π x r	r = C/ 2π	C = lunghezza circonferenzar = raggio π = 3,14 l = lunghezza arco r = raggio n = ampiezza angolo al centro A = area
Lunghezza dell'arco	l = [(2π x r)/ 360] x n	n = (l x 360)/ (2π x r)r = (l x 360)/ (2π x n)
Area del cerchio	A = π x r2
Area del settore circolare	A = [(π x r2)/360] x nA = (l x r)/ 2	n = (A x 360)/ (π x r2) l = 2A/ r r = 2A/ l
Area della corona circolare	A = π x (r12 - r22)

peso specifico definizione

1 CHILOGRAMMO è all'incirca il peso di un litro di acqua distillata a 4 gradi centigradi.

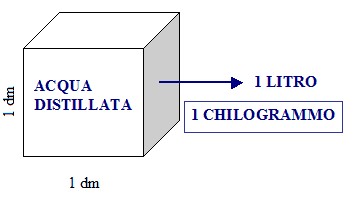
1 dm³ di acqua distillata a 4° centigradi pesa un kg. 

Se proviamo a prendere 1 dm³ di ghisa vediamo che esso non pesa un chilogrammo, bensì 7 kg e se prendiamo, ad esempio, 1 dm³ di marmo esso pesa 2,5 kg.

Possiamo allora affermare che VOLUMI UGUALI di SOSTANZE DIVERSEhanno PESO DIVERSO.

Il PESO espresso in chilogrammi di 1 dm³ di una certa sostanza prende il nome diPESO SPECIFICO e si abbrevia con la sigla ps.

Quando diciamo, ad esempio, che il peso specifico dell'argento è 10,5 significa che 1 dm³ di argento pesa 10,5 kg.

O se affermiamo che il peso specifico del rame è di 9, stiamo dicendo che 1 dm³ di rame pesa 9 kg.

  

Il PESO SPECIFICO di un corpo si ottiene DIVIDENDO il PESO del corpo stesso espresso in chilogrammi per il numero che esprime il suo VOLUME in decimetri cubi.

ps = peso : volume

possiamo anche esprimere il peso in grammi e il volume in centimetri cubi.

 Quindi, ricordiamo sempre che:

ps = peso : volume

ps = kg : dm3

ps = g : cm3

Negli esempi che abbiamo visto sopra conoscevamo il peso di un corpo e il suo volume e volevamo determinare il suo peso specifico.

Può accadere, anche, di conoscere il volume di un corpo e il suo peso specifico e di voler determinare il suo peso.

Il PESO di un corpo, espresso in chilogrammi, è uguale al PRODOTTO tra ilPESO SPECIFICO per il numero che ne misura il VOLUME in decimetri cubi.

peso = ps x volume

Anche in questo caso se il volume è espresso in centimetri cubi il peso sarà calcolato in grammi.

Infine possiamo trovarci di fronte a problemi nei quali si conosce il peso e il peso specifico di un corpo e si vuole determinare il suo volume.

Il VOLUME di un corpo, espresso in decimetri cubi, si ottiene DIVIDENDO il suo PESO espresso in chilogrammi per il suo PESO SPECIFICO.

volume = peso : ps

Anche in questo caso se il peso è espresso in grammi il volume che andremo a determinare sarà dato in centimetri cubi.

peso specifico tabella

SOLIDI		LIQUIDI
Materiale	Peso specifico	Materiale	Peso specifico
Abete	0,5	Acido solforico	1,85
Acciaio	7,85	Acqua distillata	1
Alluminio	2,7	Acqua di mare	1,03
Argento	10,5	Alcool	0,8
Catrame	1,20	Benzina	0,75
Cemento	1,40	Etere	0,74
Diamante	3,55	Latte	1,03
Ferro	7,5	Mercurio	13,6
Ghiaccio	0,92	Olio di oliva	0,9
Ghisa	7
Marmo	2,5
Oro	19,5	AERIFORMI
Piombo	11,35	Materiale	Peso specifico
Platino	21,5	Aria	0,0013
Rame	9	Ossigeno	0,0014
Sughero	0,25
Vetro	2,5